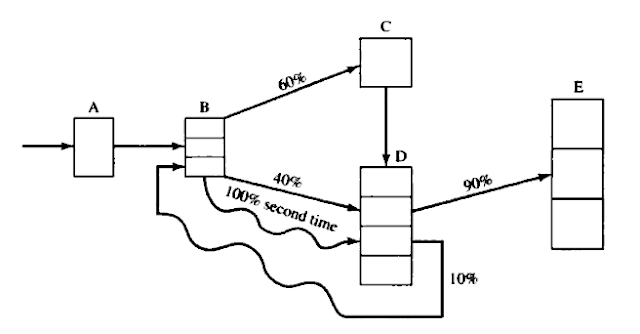
Problem: The Wee Willy Widget Shop overhauls and repair all types of widgets. The shop consists of five work stations, and the flow of jobs through the shop is as depicted here:
Regular jobs arrive at station A at the rate of one every 15 ± 13 minutes. Rush jobs arrive every 4 ± 3 hours and are given a higher priority except at station C, where they are put on a conveyor and sent through a cleaning and degreasing operation along with all other jobs. For jobs the first time through a station, processing and repair times are as follows:
The times listed above hold for all jobs that follow one of the two sequences A → B → C → D → E or A → B → D → E. However, about 10% of the jobs coming out of station D are sent back to B for further work (which takes 30 ± 10 minutes) and then are sent to D and finally to E.
Every 2 hours, beginning 1 hour after opening, the degreasing station C shuts down for routine maintenance, which takes 10 ± 1 minute. However, this routine maintenance does not begin until the current widget, if any, has completed its processing.
(a) Make three independent replications of the simulation model, where one replication equals an 8-hour simulation run, preceded by a 2-hour initialization run. The three sets of output represent three typical days. The main performance measure of interest is mean response time per job, where a response time is the total time a job spends in the shop. The shop is never empty in the morning, but the model will be empty without the initialization phase. So run the model for a 2-hour initialization period and collect statistics from time 2 hours to time 10 hours. This "warm-up" period will reduce the downward bias in the estimate of mean response time. Note that the 2-hour warm-up is a device to load a simulation model to some more realistic level than empty. From each of the three independent replications, obtain an estimate of mean response time. Also obtain an overall estimate, the sample average of the three estimates.
(b) Management is considering putting one additional worker at the busiest station (A, B, D, or E). Would this significantly improve mean response time?
(c) As an alternative to part (b), management is considering replacing machine C with a faster one that processes a widget in only 14 minutes. Would this significantly improve mean response time?
Solution: Code is written in C++ and there is also a pdf file containing the analysis for all three parts of this problem. It is available here.
The times listed above hold for all jobs that follow one of the two sequences A → B → C → D → E or A → B → D → E. However, about 10% of the jobs coming out of station D are sent back to B for further work (which takes 30 ± 10 minutes) and then are sent to D and finally to E.
Every 2 hours, beginning 1 hour after opening, the degreasing station C shuts down for routine maintenance, which takes 10 ± 1 minute. However, this routine maintenance does not begin until the current widget, if any, has completed its processing.
(a) Make three independent replications of the simulation model, where one replication equals an 8-hour simulation run, preceded by a 2-hour initialization run. The three sets of output represent three typical days. The main performance measure of interest is mean response time per job, where a response time is the total time a job spends in the shop. The shop is never empty in the morning, but the model will be empty without the initialization phase. So run the model for a 2-hour initialization period and collect statistics from time 2 hours to time 10 hours. This "warm-up" period will reduce the downward bias in the estimate of mean response time. Note that the 2-hour warm-up is a device to load a simulation model to some more realistic level than empty. From each of the three independent replications, obtain an estimate of mean response time. Also obtain an overall estimate, the sample average of the three estimates.
(b) Management is considering putting one additional worker at the busiest station (A, B, D, or E). Would this significantly improve mean response time?
(c) As an alternative to part (b), management is considering replacing machine C with a faster one that processes a widget in only 14 minutes. Would this significantly improve mean response time?
Solution: Code is written in C++ and there is also a pdf file containing the analysis for all three parts of this problem. It is available here.